Rekenen met tussenantwoorden, ook digitaal?

De afgelopen jaren is er veel gesproken over het rekenonderwijs in het mbo. Verdwijnt de centrale rekentoets? Zo ja, moeten studenten dan nog wel een rekenexamen maken? Telt het resultaat mee voor het mbo-diploma? En worden tussenstappen van het rekenproces wel of niet gewaardeerd? Nu is er meer duidelijkheid over het rekenbeleid. Er zijn nieuwe rekeneisen ontwikkeld en daarnaast is er een coöperatie opgericht die verantwoordelijk is voor de ontwikkeling van nieuwe rekenexamens. Het voornemen is dat het vak rekenen vanaf het schooljaar 2022-2023 onderdeel uitmaakt van het kwalificatiedossier en meetelt voor het diploma.
Ondanks de afschaffing van de centrale rekentoets blijft het ontwikkelen en onderhouden van de rekenvaardigheid belangrijk. De centrale rekentoets wordt vervangen door een instellingsexamen. Door deze aanpassing van het rekenbeleid, mogen mbo’s zelf bepalen op welke manier zij toetsen of studenten aan de rekeneisen voldoen. Kortom, de komst van het instellingsexamen rekenen maakt het mogelijk om op een andere manier te toetsen dan voorheen. Het afgelopen jaar heeft Bureau ICE in samenwerking met AlgebraKiT en het onderwijsveld onderzoek gedaan naar een alternatieve manier van digitale toetsing. We hebben een toetsvorm ontwikkeld waarbij niet alleen het eindantwoord op een opgave centraal staat, maar ook de rekenstappen die een student maakt om tot het eindantwoord te komen. Het toetsprogramma valideert namelijk naast het eindantwoord ook de tussenantwoorden die een student geeft. Deze nieuwe manier van toetsing biedt een aantal voordelen, waaronder:
- De berekeningen en tussenantwoorden worden opgeslagen. Door deze na de toetsafname te analyseren, kan een docent gerichte feedback geven.
- Als een student bijvoorbeeld de eerste helft van een opgave correct uitrekent, krijgt hij wel enkele punten voor deze rekenstappen.
Digitale rekentoets met tussenantwoorden
Bij de huidige centrale rekentoets wordt enkel het eindantwoord gewaardeerd en worden geen deelpunten toegekend aan correcte tussenstappen. Door deze beperkte manier van toetsing wordt niet inzichtelijk welke rekenstrategie studenten gebruiken en waar ze eventueel fouten maken. Door het gebruik van AlgebraKiT is het mogelijk om ook in digitale toetsen tussenantwoorden te waarderen. Zowel voor formatieve als summatieve toetsing heeft dit een meerwaarde. Twee voordelen zijn hierboven al benoemd.
Bij formatieve toetsing speelt vooral het eerst benoemde voordeel een belangrijke rol. Als een toets met AlgebraKiT formatief wordt ingezet, zie je als docent welke strategie een student heeft gebruikt en waar eventueel fouten gemaakt worden in het rekenproces. Deze informatie kan vervolgens gebruikt worden bij het geven van passende feedback.
Bij summatieve toetsing speelt juist het tweede voordeel een belangrijke rol. Als de toets met AlgebraKiT summatief wordt ingezet, meet je nauwkeuriger wat de student wel en niet kan. Wij vinden dit een eerlijkere manier van meten.
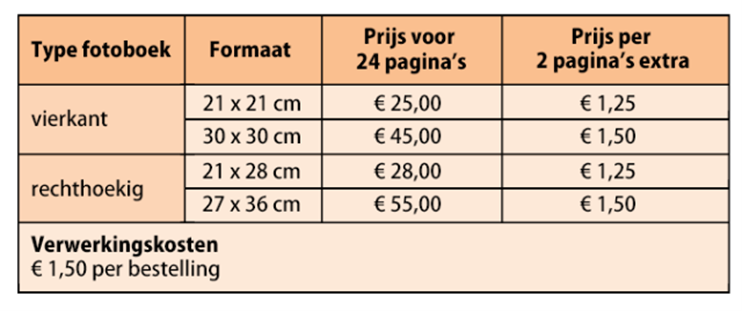
Tabel 1 laat een voorbeeldopgave zien uit een digitale rekentoets met tussenantwoorden. Ook is hier de beoordeling achteraf te zien. In het systeem is onder iedere contextopgave een digitaal kladpapier opgenomen. De student noteert hierop de berekening met of zonder toelichting. Het systeem analyseert na afloop van de toets welke tussenantwoorden correct zijn en waar eventuele fouten zijn gemaakt in het rekenproces. In de beoordeling kan de docent zien welke tussenantwoorden door het systeem als correct zijn beoordeeld en waar de student in het rekenproces een fout heeft gemaakt.
Voorbeeldopgave met bijbehorende uitwerking en beoordeling achteraf
Voorbeeldopgave 1
Veerle bestelt een rechthoekig fotoboek van 27 x 36 cm. Het fotoboek heeft in totaal 30 pagina’s.
Hoeveel moet Veerle in totaal betalen?
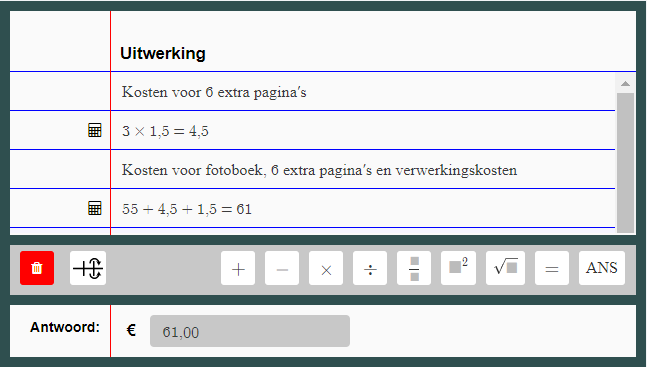
Correcte uitwerking met toelichting
In het onderstaande voorbeeld is te zien op welke manier een student de opgave heeft uitgerekend. De student heeft naast de formele berekening ook zijn rekenstappen toegelicht.
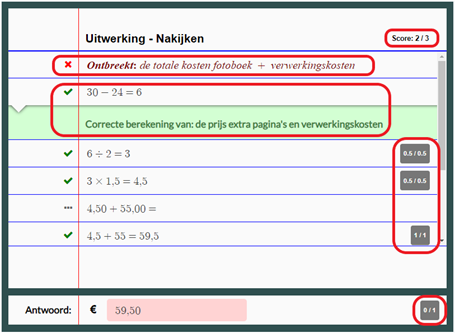
Beoordeling van een deels correcte berekening
In het onderstaande voorbeeld is te zien dat de student 2 van de 3 punten heeft behaald en welke tussenstappen deze 2 punten opleverden. De ontbrekende stap is ook aangegeven: de student heeft de verwerkingskosten niet bij de kosten van het fotoboek opgeteld. Door op de groene vinkjes te klikken, komt er een toelichting bij de tussenantwoorden te staan.
Denkactiviteiten gekoppeld aan digitale rekentoets met tussenantwoorden
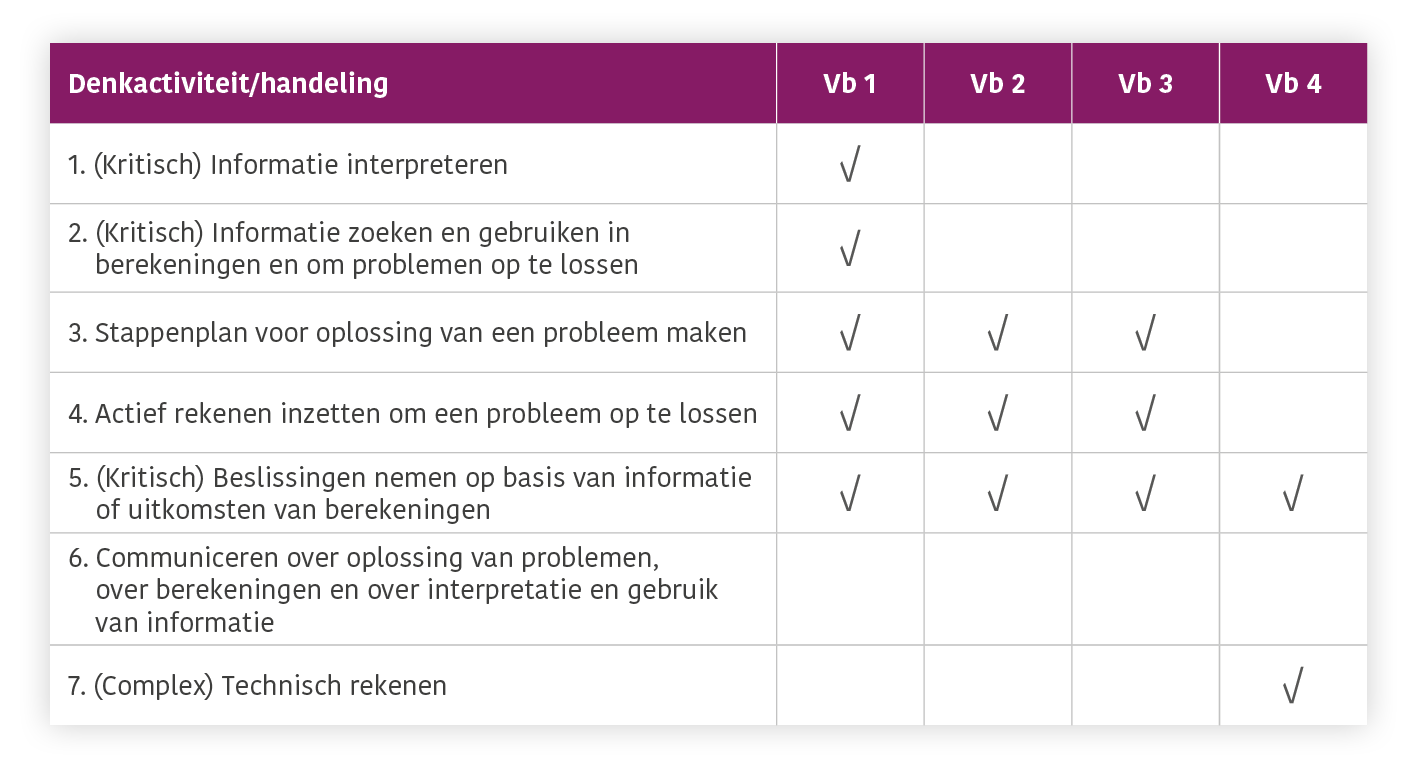
In de nieuwe rekeneisen voor het mbo worden zeven denkactiviteiten en handelingen benoemd (Expertgroep Herijking Rekeneisen mbo, 2020 [1]). Hieronder laten we aan de hand van vier voorbeeldopgaven zien hoe deze te relateren zijn aan opgaven in een digitale rekentoets waarbij tussenantwoorden worden gewaardeerd. In Tabel 1 staat voorbeeldopgave 1. De andere drie voorbeeldopgaven staan hieronder.
Tabel 2. Zeven denkactiviteiten en handelingen in het rekenonderwijs gekoppeld aan een digitale rekentoets met tussenantwoorden
Voorbeeldopgave 2
Karen doet mee aan een hardloopwedstrijd van 15 km. Ze doet hier 1 uur en 20 minuten over.
Hoeveel kilometer per uur was de gemiddelde snelheid van Karen?
Rond je antwoord af op één decimaal.
Voorbeeldopgave 3
Lydia legt nieuwe tapijttegel in haar slaapkamer. De slaapkamer is 4,2 bij 3,5 m. Eén tapijttegel is 50 cm bij 30 cm.
Hoeveel tapijttegels heeft Lydia minimaal nodig?
Voorbeeldopgave 4
64 : 100 = ________
(Kritisch) Informatie interpreteren en (kritisch) Informatie zoeken en gebruiken in berekeningen en om problemen op te lossen
De eerste denkactiviteit is het kritisch interpreteren van informatie. Dit hangt nauw samen met de tweede denkactiviteit waarbij studenten informatie op moeten zoeken en vervolgens moeten gebruiken bij het uitvoeren van een berekening. Beide denkactiviteiten worden vooral bevraagd bij opgaven behorende bij het domein ‘omgaan met kwantitatieve informatie’. Om voorbeeldopgave 1 te kunnen beantwoorden moet de student de benodigde informatie opzoeken in de tabel. Hij moet kritisch kijken welke informatie hij nodig heeft en daarnaast ook interpreteren hoe bepaalde informatie gecombineerd moet worden. Bij een digitale toets met tussenantwoorden kan een student laten zien dat hij hiertoe in staat is. In een digitale toets zonder tussenantwoorden heeft een student deze vaardigheid ook nodig, maar is het niet inzichtelijk voor een docent of eventuele fouten gemaakt worden door het aflezen van de kwantitatieve informatie of dat de fout op een ander moment in het rekenproces is gemaakt.
Stappenplan voor oplossing van een probleem maken en actief rekenen inzetten om een probleem op te lossen
De derde handeling ‘een stappenplan maken’ is vaak nodig bij het uitrekenen van contextopgaven en in minder mate bij contextloze opgaven. Bij voorbeeldopgave 1 tot en met 3 kan een student het rekenprobleem alleen oplossen als hij vooraf en tijdens de berekening nadenkt welke stappen hij moet nemen om tot het antwoord te komen. Om vervolgens tot een antwoord te komen, komt de vierde handeling ‘actief rekenen’ aan de orde. Het wel of niet beheersen van deze vaardigheden wordt voor de docent na de afname van een digitale toets met tussenantwoorden inzichtelijk. In de toetsresultaten kan hij namelijk zien welke stappen een student heeft genomen om tot het antwoord te komen. Bij een digitale rekentoets zonder tussenantwoorden wordt het voor de docent alleen inzichtelijk of een student deze vaardigheden beheerst als de student een correct eindantwoord geeft. Als het eindantwoord fout is, is de oorzaak van de fout lastig te achterhalen.
Beslissingen nemen op basis van informatie of uitkomsten van berekeningen
Kritisch beslissingen nemen op basis van de uitkomst is de vijfde denkactiviteit. In de toetsresultaten van studenten zien we regelmatig terug dat studenten hier moeite mee hebben of dit zelfs vergeten. Ze reflecteren onvoldoende of het gegeven antwoord past bij de vraagstelling. Deze vaardigheid heeft een student, volgens ons, bij elke contextvraag in een digitale rekentoets nodig. Bijvoorbeeld bij voorbeeldopgave 2: als een student hier antwoordt dat Karen 11.250 kilometer per uur hardloopt, moet hij zich afvragen of dit antwoord wel passend is bij de gegeven context. Deze vaardigheid wordt door iedere vorm van (digitale) toetsing inzichtelijk, doordat een docent achteraf het gegeven antwoord naast de vraagstelling kan leggen.
Communiceren over oplossing van problemen, over berekeningen en over interpretatie en gebruik van informatie
De een na laatste denkactiviteit, waar het communiceren over de oplossing onder valt, is minder passend bij een digitale rekentoets met tussenantwoorden. De student kan op het kladpapier wel opschrijven welke rekenstappen hij neemt, maar dit is niet volledig vergelijkbaar met het mondeling overbrengen. Dit is de enige denkactiviteit die minder geschikt is om in beeld te brengen met een digitale toets.
(Complex) Technisch rekenen
Tot slot, de zevende handeling ‘technisch rekenen’. Onder technisch rekenen verstaan wij het uitrekenen van opgaven zonder context. De digitale rekentoetsen in TOA bestaan uit opgaven met context en opgaven zonder context, ook wel contextloze opgaven. De contextloze opgaven, zoals voorbeeld 4, zijn uitermate geschikt om de technische rekenvaardigheid aan te tonen. Dit kan zowel in een reguliere digitale rekentoets als in een rekentoets met tussenantwoorden aangetoond worden, omdat deze opgaven in veel gevallen uit het hoofd of eventueel in combinatie met kladpapier uitgerekend zullen worden.
Kortom, een digitale rekentoets met tussenantwoorden vraagt 6 van de 7 denkvaardigheden van een student. In vergelijking met een digitale rekentoets zonder tussenantwoorden is dit aanzienlijk meer. Naast dat 6 van de 7 denkvaardigheden in beeld worden gebracht door een digitale rekentoets met tussenantwoorden, heeft het ook dezelfde voordelen als een reguliere digitale rekentoets, zoals weinig voorbereidingstijd, flexibel toetsen en geen nakijktijd. Een digitale rekentoets met tussenantwoorden is hierdoor een efficiënte manier om inzicht te krijgen in de rekenvaardigheid en gebruikte rekenstrategieën van studenten.
[1] https://taalenrekenenmbo.nl/app/uploads/Advies-rekeneisen-MBO_WEB.pdf
Neem deel aan de pilot ‘Rekenen met tussenantwoorden’
Heb jij als docent interesse in deze manier van toetsen? Doe mee aan de pilot en maak kennis met deze nieuwe toetsvorm. Lees hier meer en vul het formulier in.